【保存版】幾何公差とは？記号一覧と意味からルールまでわかりやすく解説！

本ページには広告が含まれています

図面に書かれている「真直度」「位置度」などの幾何公差記号、意味が分からず悩んでいませんか？

幾何公差は製品の精度や品質を左右する、設計上欠かせないルールのひとつです。

とはいえ、記号の種類や意味、記入方法など、初めて触れると戸惑う内容が多いのも事実。

特に初心者の方にとっては、どこから理解すればいいのか迷いやすいポイントなんですよね。

でも大丈夫！

この記事では、そんなお悩みをまるごと解決できるように、以下のような内容をやさしく丁寧に解説しています。

• 幾何公差とは？寸法公差との違いと役割を解説
• 幾何公差の記号一覧と意味、4つの分類の覚え方
• 図面における幾何公差の記入ルールと見方
• 実務での注意点と、失敗しないための選定ポイント

基礎から図面実例までしっかりカバーしているので、幾何公差に自信を持って対応できるようになりますよ！

幾何公差とは？初心者でもわかる基本の意味と役割

図面に幾何公差の記号が書いてあっても、意味や役割が分からないと使いこなせません。

ここではまず、定義と役割を明確にし、寸法公差との違いを通じて「幾何公差の必要性」をしっかり理解していきましょう。

■ 幾何公差の定義

幾何公差とは、部品の形状・姿勢・位置・振れなどのズレを数値で制限するための設計ルールです。

例えば、

「この面はできるだけ平らであること」
「この穴は正しい位置にあること」

といったように、形そのものの誤差に対して許容範囲を明示するのが幾何公差の役割なんですよね。

寸法の「長さ」だけを見ていては判断できないズレを、設計段階でしっかり管理するために使われています。

■ 寸法公差との違いで分かる役割

幾何公差の理解には、寸法公差との違いを比較するのがいちばん分かりやすい方法。

以下の表を見れば、それぞれがカバーしている領域の違いが一目でわかります。

比較項目	寸法公差	幾何公差
管理対象	長さ・直径などのサイズ	形状・傾き・位置などのかたち
目的	サイズ誤差の抑制	形のズレ・組立精度の保証
図面記号	±記号（例：φ10±0.1）	特殊な図記号（例：⊥、○、｜など）
使われる場面	加工寸法の範囲を指定したい時	組立や動作精度を保ちたい時

寸法公差は「大きさ」の制御、幾何公差は「かたち」の制御。

この2つを組み合わせることで、精密な設計や高品質な製品づくりが可能になります。

■ なぜ幾何公差が必要なのか？

たとえば、シャフトと穴の部品を組み合わせる場面を想像してみてください。

寸法はぴったりでも、軸が少し斜めになっていたら、スムーズに動かない、うまくはまらないといったトラブルが起こるかもしれません。

このような問題は、寸法公差では管理しきれない「位置や傾きのズレ」が原因。

幾何公差を設計段階で正しく指定すれば、こうした微妙なズレを抑え、トラブルを未然に防ぐことができます。

結果として、不良率の低下・加工コストの削減・製品寿命の向上にもつながるんですよね。

つまり幾何公差は、品質と機能を支える「見えない設計の柱」といえるでしょう。

幾何公差の記号一覧と分類まとめ

幾何公差には多くの種類がありますが、すべては4つの分類に整理されています。

この分類を押さえることで、記号の意味や使いどころもぐっと理解しやすくなりますよ。

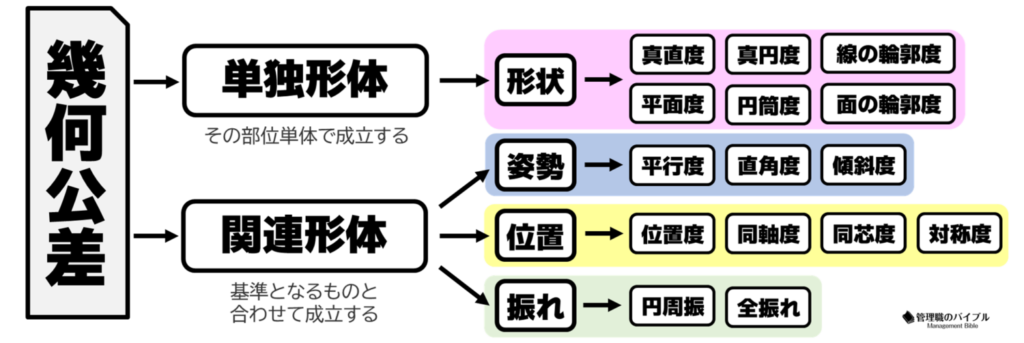
分類①： 形状公差｜部品そのものの“形の精度”を管理する公差

形状公差は、基準となるデータム（基準面や線）を必要とせず、単独で部品の形状そのものを評価する公差。

「どれだけまっすぐか」「どれだけ真円に近いか」「表面がどれだけキレイに整っているか」など、見た目や動きに直結する“かたちの正確さ”を評価するのがこの分類の役割です。

公差名	記号	管理対象	内容
真直度		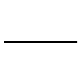線・軸	対象とする直線形体が「どの程度正確に真っ直ぐか」の許容を表したもの
平面度		面	対象とする平面が「どの程度滑らかで均一性があるか」の許容を表したもの
真円度		円の断面	対象とする円形形体が「どの程度正確に真ん丸か」の許容を表したもの
円筒度		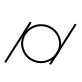円筒全体	対象とする円筒形体が「どの程度真ん丸で真っ直ぐか」の許容を表したもの
線の輪郭度		曲線	対象とする断面の曲線が「正確に指示した曲線になっているか」の許容を表したもの
面の輪郭度		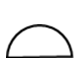曲面	対象とする面全体が「正確に指示した曲面になっているか」の許容を表したもの

たとえば、モーターシャフトやベアリング軸など、滑らかに動く構造では「真直度」や「円筒度」が非常に重要になります。

「見た目が丸ければOK」ではなく、測定器で確認された数値で“合格かどうか”を判断するのが幾何公差の考え方。

この分類を正しく理解しておくと、「なぜこの公差が必要なのか」を現場でも説明できるようになります。

分類②： 姿勢公差｜基準に対して“どのような向き”であるかを管理する公差

姿勢公差は、部品の線や面が「基準面（データム）」に対して、どのような角度・姿勢を保っているかを評価するための公差。

形状そのものではなく、「基準と比べてどれだけ平行か、直角か、傾いていないか」をチェックするために使われます。

見た目では判断しにくい、姿勢の精度を数値で示すのが特徴。

部品同士を正しく組み合わせるには、この“姿勢”の正確さが欠かせないんですよね。

公差名	記号	管理対象	内容
平行度		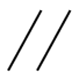線・面	データムに対して直線または平面が「どの程度平行であるか」の許容を表したもの
直角度		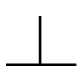線・面	データムに対して「どの程度正確に直角であるか」の許容を表したもの
傾斜度		線・面	データムに対して90°以外で「どのくらい正確に傾斜しているか」の許容を表したもの

たとえば、組立部品が少しでも斜めに傾いていたら、他の部品と噛み合わなくなるかもしれません。

そうしたズレを避けるため、基準に対して“正しい向き”で加工されているかを確認するのが姿勢公差の役割です。

実際には、「この穴は基準面と直角に」「この面はあの面に対して5度傾けて」といったように、意図を具体的に図面へ伝えるための記号として使用。

姿勢が狂えば、製品全体のバランスにも影響します。

分類③： 位置公差｜穴や軸の“位置ズレ”を正確にコントロールする公差

位置公差は、部品に空いた穴や軸の中心が、基準に対してどれだけ正しい位置にあるかを評価するための公差です。

位置精度そのものを管理するための設計指針。

この分類では、形状や角度ではなく「中心点のズレ」に注目し、それを制御することが目的になります。

見た目では分からないけれど、組立精度や機能性に大きく関わる要素なんですよね。

公差名	記号	管理対象	内容
位置度		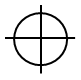穴・軸中心	データムに対して「どのくらい正確な位置にあるか」の許容を表したもの
同軸度		複数軸	データム軸直線に対して「中心軸がずれていないか」の許容を表したもの
同心度		円形部品	断面で見た時のデータム中心点に対して対象の「中心点がずれていないか」の許容を表したもの
対称度		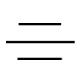対称形状	データムに対して「どの程度対称の位置関係にあるか」の許容を表したもの

たとえば、シャフトとハウジングの中心がズレていたら、回転時に異音や摩耗の原因になってしまいます。

さらに、穴の位置が少しでもズレていれば、部品がうまく組み合わないというトラブルが起きることも…

そんな問題を防ぐために使われるのが位置公差。

基準に対して“正しい中心の位置”を保証することで、スムーズな組立と安定した動作につながります。

分類④： 振れ公差｜回転部品の“ブレ”を評価するための公差

振れ公差は、回転する部品の揺れやブレを測定し、どれだけ安定して回転できるかを評価する公差。

この分類は、特にモーターやベアリング、シャフトなどの回転部品の性能・寿命に直結する非常に重要な指標です。

公差名	記号	管理対象	内容
円周振れ		外周点	データム軸を中心として、「部品を回転させたときの任意の円周の一部の振れ」の許容を表したもの
全振れ		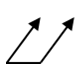全外周	データム軸を中心として、「部品を回転させたときの表面全体の振れ」の許容を表したもの

たとえば、回転中にブレがあると、部品がぶつかったり、異常振動を起こしたりする恐れがあります。

こうした不具合は、寸法や位置だけでは防げない“回転の精度”の問題がほとんど。

振れ公差を設計に取り入れることで、高回転時の安定性・静音性・耐久性を確保できます。

幾何公差の更に詳しい解説

幾何公差は、記号を知っているだけでは不十分。

それぞれの意味や使い方を正しく理解することで、図面の意図がしっかり読み取れるようになります。

---

真直度

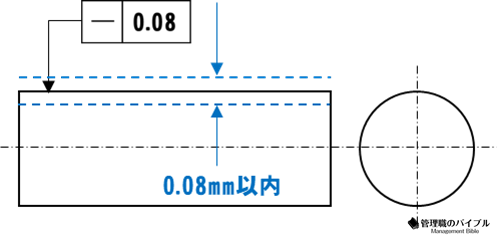
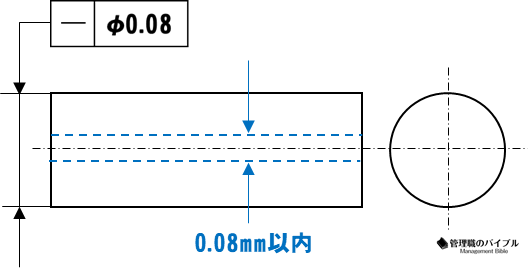
真直度は、線や軸がどれだけまっすぐであるかを評価する幾何公差です。

曲がりやたわみの管理に用いられる基本的な要素。

軸がわずかに歪んでいるだけでも、回転時に振動や摩耗を引き起こす可能性があります。

そのため、直進性の精度を数値で保証する必要があるんですよね。

評価対象は線状の形状で、JISでは基準なしで単独評価が可能とされています。

測定には、ダイヤルゲージや三次元測定機を使用するのが一般的。

---

平面度

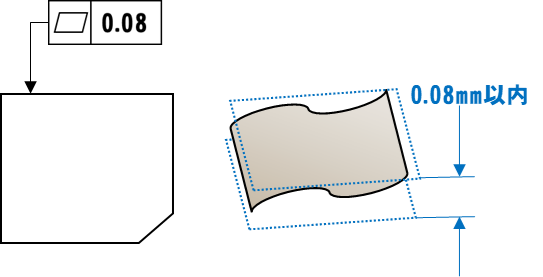
平面度は、ある面が理想の平面からどれだけズレていないかを評価する公差。

凹凸や反りの有無を判断する基準になります。

たとえば、部品の接地面が歪んでいると、組み立て後にガタつきやズレが生じることも。

その防止のために、面全体の“平らさ”を数値で管理します。

基準面は不要で、単独での評価が可能。

測定には、光学式の平面度測定器や三次元測定機がよく使われます。

---

真円度

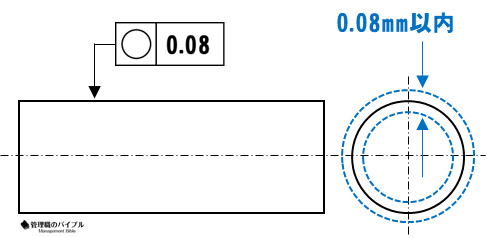
真円度は、断面の形状が理想の円からどれだけ外れているかを測定する公差。

穴や軸の円形断面に適用されます。

この公差により、偏摩耗や回転時の振動を未然に防ぐことが可能。

結果として、長期的な信頼性や性能向上につながります。

1断面上で評価され、全周の点が一定の公差帯内にある必要があります。

精密部品では特に重視される要素と言えるでしょう。

---

円筒度

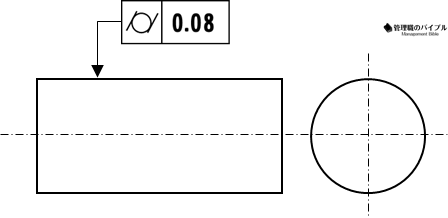
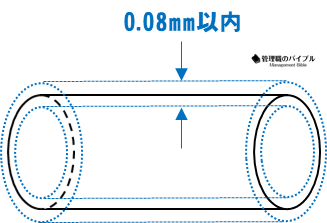
真直度は、線や軸がどれだけまっすぐであるかを評価する幾何公差です。

曲がりやたわみの管理に用いられる基本的な要素。

軸がわずかに歪んでいるだけでも、回転時に振動や摩耗を引き起こす可能性があります。

そのため、直進性の精度を数値で保証する必要があるんですよね。

評価対象は線状の形状で、JISでは基準なしで単独評価が可能とされています。

測定には、ダイヤルゲージや三次元測定機を使用するのが一般的。

---

線の輪郭度

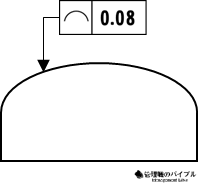
線の輪郭度は、曲線が意図した通りの形状で加工されているかを評価する公差。

平面内の輪郭精度を確認するために使われます。

特に自由曲線や装飾性の高い部品では、形状のズレが外観や機能に直結することも。

そのため、公差による管理が欠かせないんですよね。

対象線のすべての点が、公差帯内に収まっている必要があります。

形状の一貫性を担保するための重要な指標と言えるでしょう。

---

面の輪郭度

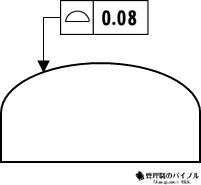
面の輪郭度は、曲面や複雑な形状の面が設計通りに仕上がっているかを評価する公差。

三次元的な自由曲面に対して使用します。

たとえば、金型や外装部品では、微妙な凹凸が性能や見た目に大きく影響。

対象となる面のすべての点が、公差帯の中に含まれていることが求められます。

高精度加工では必須の公差と言えるでしょう。

---

平行度

平行度は、対象となる線や面が、基準要素とどれだけ平行であるかを評価する公差です。

見た目では判断できない微細な傾きを数値で管理するために使用。

たとえば、スライドレールの上下がズレていた場合、動作不良や偏摩耗が発生します。

それを防ぐために、精度の高い“並行”を維持する必要があるんですよね。

対象は平面・線どちらでも可能で、姿勢公差に分類されます。

基準に対する向きの精度を保証するための指標と言えるでしょう。

---

直角度

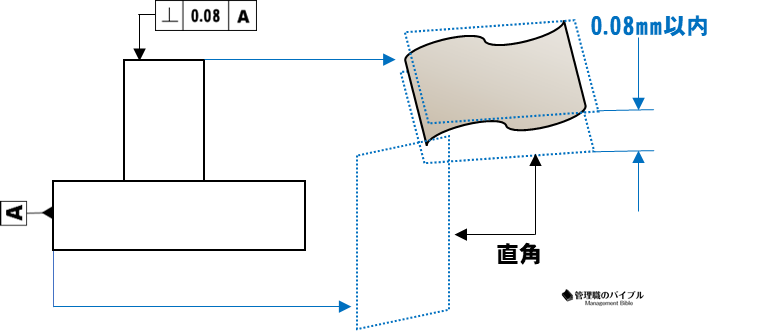
直角度は姿勢公差の一つで、ある面や線が、基準に対してどれだけ直角になっているかを示す公差です。

部品の組立精度や立ち上がり角の管理に欠かせない要素。

たとえば、基準面に対して垂直なボルト穴がズレていれば、しっかり固定できず構造全体に影響が及びます。

そのリスクを回避するには、角度の精度管理が必要不可欠。

高精度な直角性を求める場面で活用されます。

---

傾斜度

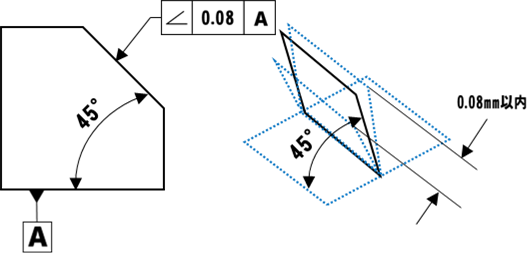
傾斜度は、対象となる線や面が、基準に対して設定された角度で傾いているかを評価する公差です。

直角・平行以外の角度に対して指定。

たとえば、刃先の傾きや斜めのガイド部などは、わずかな角度のズレでも性能に影響が出ることがあります。

その精度を維持するためには、角度の許容範囲を数値で明確にすることが必要不可欠。

この公差も姿勢公差に分類され、製品設計の自由度を保ちながら精度を確保できる利点があります。

傾きのコントロールに特化した管理手法と言えるでしょう。

---

位置度

位置度は、穴や軸の中心が、基準に対してどれだけ正確な位置にあるかを評価する幾何公差。

寸法通りの加工がされているかを確認するために使われます。

たとえば、ボルト穴がずれていた場合、部品がうまく組み合わず、干渉や性能低下の原因になりかねません。

そのリスクを避けるために、中心位置の精度が重要になります。

対象の中心と理想位置のずれを数値で制御することで、組立精度を確保。

位置公差の基本とも言える存在です。

---

同軸度

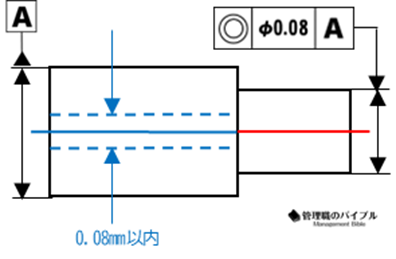
同軸度は、複数の軸状形状が、同じ中心軸上にあるかを評価する公差です。

外径と内径などが共通軸を持っているかを判断。

軸の中心が少しでもずれていると、回転時に異音や振動、摩耗が発生してしまいます。

そのため、複数の軸が一体として回転する部品では特に重視されるんですよね。

評価対象は円筒形状に限定され、回転精度の確保が目的。

回転体の性能と寿命に大きく関わる要素です。

---

同心度

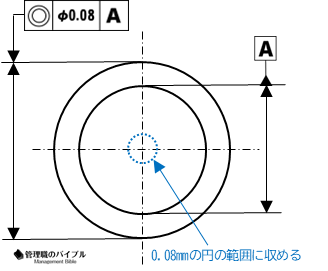
同心度は、複数の円形形状の中心点が、どれだけ一致しているかを示す幾何公差。

見た目では分かりづらい精密な中心のずれを制御します。

たとえば、ハウジングとシャフトの内径と外径が同心でなければ、回転に支障をきたすことも。

正確な中心の一致が求められます。

同軸度との違いは、評価基準が“中心点”にあること。

より厳密な位置精度を求める設計で使われます。

---

対称度

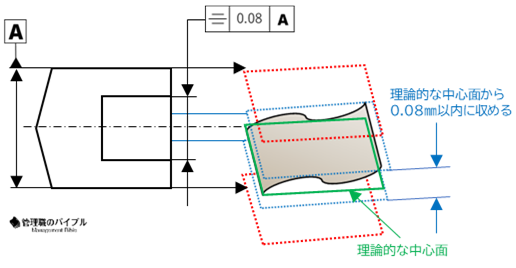
対称度は、対象形状が基準線や基準面に対して、どれだけ対称になっているかを評価する公差。

見た目だけでなく機能面でも左右バランスが重要な部品に使われます。

たとえば、左右対称の筐体で中心からのズレがあると、重心が偏り、性能や美観に悪影響が出ることも。

そういったズレを防ぐための指標が対称度です。

評価対象は形状全体。

バランスを維持するための公差管理が求められます。

---

円周振れ

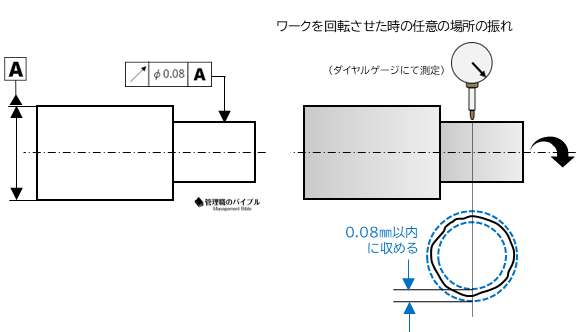
円周振れは、回転中に任意の1点がどれだけブレるかを評価する幾何公差です。

主に回転部品の精度確保に使用。

たとえば、シャフトの表面にわずかなブレがあると、機械全体の振動や騒音につながる可能性があります。

それを抑えるために、1点の揺れ幅を数値で管理することが必要不可欠。

測定は基準軸に対して行われ、主に外周の一点を基準に評価。

組立精度と回転安定性の指標となる要素です。

---

全振れ

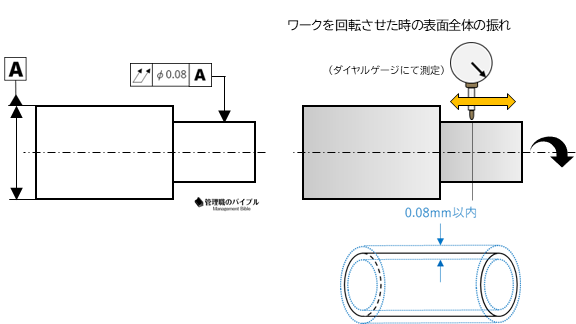
全振れは、回転部品の全表面がどれだけブレているかを評価する公差です。

円周振れとは異なり、軸方向と円周方向の両方を統合して評価。

たとえば、工具の回転ブレや測定機の軸ブレは、作業精度や測定誤差に直結します。

それらを包括的に抑えるためには、全振れの制御が必要不可欠。

対象は全周の表面と軸方向で、最も厳密な回転精度管理を行う際に使われます。

---

図面での幾何公差の記入ルールと読み方

■ 幾何公差の表し方とは？？

下の図の赤丸部分が幾何公差です。

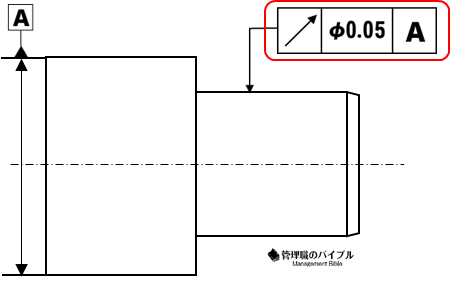
四角のボックスが並んでおり、それぞれのボックスに以下のものが入ります。

• 左側のボックスには「幾何公差記号」
• 真ん中のボックスには「ばらつきの許容差」
• 右側のボックスには「データム記号」

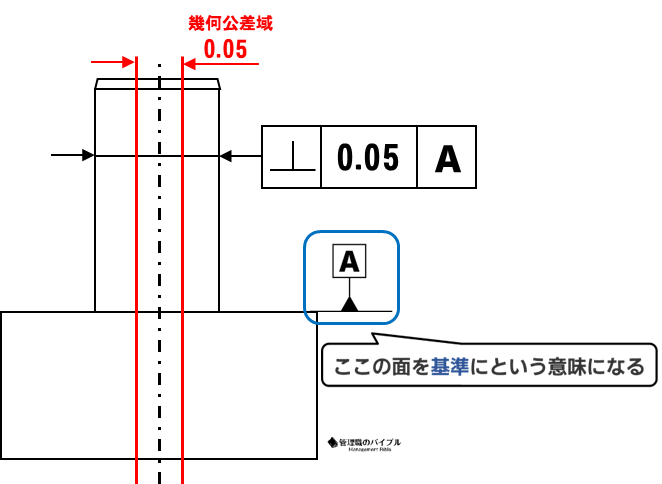
■ データムとは？？

データムとは、加工や寸法測定をする場合に基準とする面または線・点のこと。

「ここが基準の場所ですよ！」という意味になります。

■ データムが必要な時、不必要な時

幾何公差は大きく分けて「単独形体」と「関連形体」の２つがあります。

「単独形体」とは、他の要素を基準にせず、対象の形状そのものに対して公差を与えるタイプの幾何公差。

この場合、データム（基準）は必要ありません。

逆に「関連形体」とは、他の基準（データム）に対して相対的な位置や向きを評価する幾何公差。

つまり、必ずデータムの指定が必要になります。

① 単独形体

その形状自体に幾何公差が指定できる

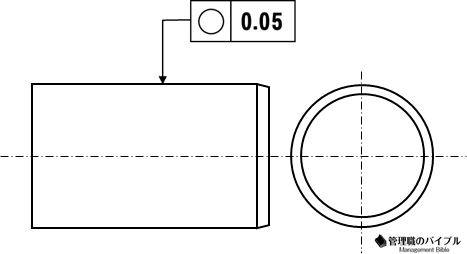
上記の「真円度」は単独形体なので…

データムは不要

② 関連形体

データムとの関係を指定する

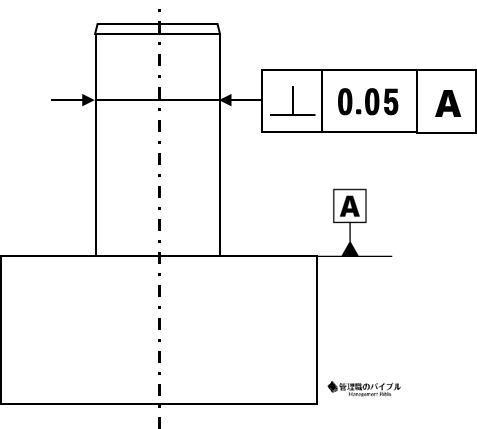
直角度のよう関連形体を表す際は

基準（データム）となる面や線が必要！

■ データム記号の記入方法

データム記号はどこでも適当に書いていいわけではなく、ちゃんとルールがあります。

データムは指す場所によって基準の場所が変わるのが特徴。

寸法線の延長戦上にデータムがある時

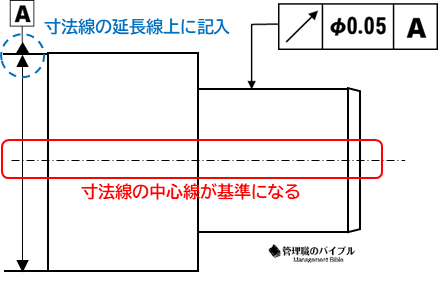
この場合は寸法線の中心線が基準となります

図形に直接データムがある時

この場合は指定箇所そのものが基準となります

■ 幾何公差の記入方法

幾何公差もデータムと同じく指す場所によって基準の場所が変わってきます。

データムと同じ法則なので覚えておきましょう。

寸法線の延長戦上に幾何公差の指示がある時

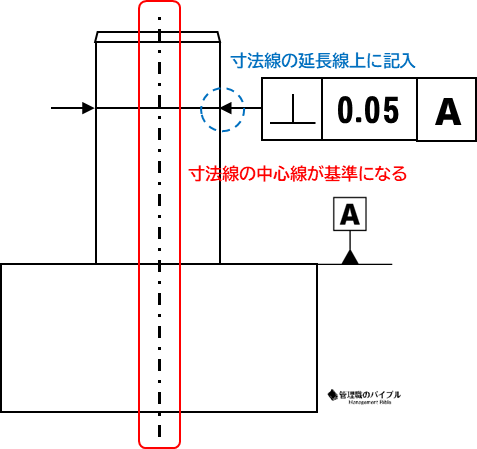
この場合は寸法線の中心線が基準となります

図形に直接、幾何公差の指示がある時

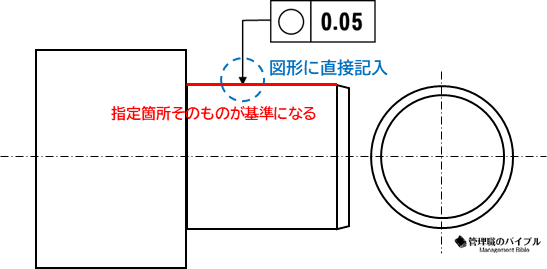
この場合は指定箇所そのものが基準となります

幾何公差で失敗しないための注意点！

幾何公差は精密設計の要。

小さな設定ミスが大きな不良やコスト増につながるため、よくある失敗と注意点を事前に押さえておきましょう。

■ 不必要な幾何公差を指定しない

すべての形状に幾何公差を付ける必要はありません。

意味のない指定をすると、測定や加工の手間が増え、無駄なコストを招くリスクがあります。

たとえば、見た目に影響しない裏面にまで厳しい平面度を指定してしまうと、必要以上に加工精度を求められることに。

その結果、製品価格や納期に影響するケースもあるんです。

■ データムの設定順序を誤らない

データムは幾何公差を評価する際の基準となるため、設定順序が非常に重要。

たとえば「A → B → C」とすべきところを「C → B → A」としただけで、測定結果がまったく変わってしまいます。

基準面・基準線・基準点の意味を理解し、図面ごとに最も安定した測定ができる順序を選ぶことが大切ですよ。

■ 寸法公差と幾何公差の整合性

寸法公差だけで管理している場合、幾何公差との整合性が取れていないと矛盾が発生することもあります。

たとえば、寸法では±0.1mmとしながら、位置度で0.05mm以内と指定してしまうと、設計意図が曖昧になってしまうケースも…。

両者の関係性を理解し、明確で一貫性のある設計を意識する必要があります。

■ 測定可能かどうかを考慮する

幾何公差を指定する際には、実際に測定できるかどうかも忘れずに考えましょう。

特殊な形状や微細な公差は、高額な測定機器が必要になることもあるため、現場の測定環境に合った指定が大切。

設計段階から測定工程までを見据えた公差設計は、製品開発全体の最適化につながります。

■ 加工現場との情報共有

図面上で正しく指定していても、現場との認識にズレがあると意味がありません。

幾何公差は記号やルールが複雑なため、意図や測定方法までを具体的に伝えるコミュニケーションが不可欠。

ミスや不具合を防ぐには、設計者と製造側が一体となった情報共有が鍵になります。

---

幾何公差のおすすめ教育方法

幾何公差はルールが多く、図面に関わる人すべてが正しく理解しておく必要があります。

ですが、種類も多く、他に人にどう教育していくのかは悩みどころ。

そこでおすすめしたいのが、社内教育に最適な「幾何公差の基礎知識」という台本付きのパワーポイント教材です。

＼ 期間限定50％OFFの大特価！ ／

¥7,990 通常価格 ▶ ▶ ▶ ¥3,995 税込

「幾何公差の基礎知識」は、幾何公差に苦手意識を持つ人にも安心して使えるパワーポイント形式の教材。

講義の進行に必要なスライドと、読み上げ用の台本がセットになっているので、資料をそのまま使って誰でも講師役を務められるのが大きな特徴です。

構成は5章立てで、幾何公差の定義から記号ルール、各公差の種類と意味までを丁寧に解説。

特に図解が豊富で、視覚的にイメージを掴みやすく、社内の教育資料として非常に使いやすい内容になっています。

また、現場で役立つ「幾何公差一覧表」の付録もあり、研修後も継続的に参照できる点も嬉しいポイント。

設計者だけでなく、製造や検査に関わる人たちにも広くおすすめできる教材といえるでしょう。

＼ 20分で幾何公差を習得できる ／

幾何公差の基礎知識を購入

多くの企業に喜ばれています！

【たった20分】幾何公差をパワ－ポイントで社内教育！コスパ最強の資料を紹介！

幾何公差の社内教育に悩んでいる現場リーダー・教育担当者の方は必見！この記事では、準備ゼロ・たった20分で教えられる「台本付きパワーポイント教材」の活用法をご紹介。図解豊富で初心者にも伝わりやすく、繰り返し使える実用性の高さが現場で大好評です！

まとめ：幾何公差の理解が“精度と信頼”を生む設計力につながる！

幾何公差は、ただの記号ではありません。

それぞれに明確な意味と目的があり、正しく使いこなすことで、設計の精度は格段に高まります。

この記事では、その基本から記号の読み方、記入ルール、失敗しないコツまでを丁寧に解説してきました。

もし「社内で幾何公差を教えるのが難しい…」と感じているなら、台本付きのパワーポイント教材「幾何公差の基礎知識」が心強い味方になります。

誰でも講師になれる構成で、短時間でも伝わる研修を実現できる内容。

設計と現場のズレをなくし、品質トラブルを防ぐためにも、今こそ幾何公差の“正しい学び”を始めてみませんか？

＼ 20分で幾何公差を習得できる ／

幾何公差の基礎知識を購入

多くの企業に喜ばれています！

【たった20分】幾何公差をパワ－ポイントで社内教育！コスパ最強の資料を紹介！

幾何公差の社内教育に悩んでいる現場リーダー・教育担当者の方は必見！この記事では、準備ゼロ・たった20分で教えられる「台本付きパワーポイント教材」の活用法をご紹介。図解豊富で初心者にも伝わりやすく、繰り返し使える実用性の高さが現場で大好評です！